Batch 2 - Class 31 - Visualizing Identities, Pirate Puzzles

• MartinShCol 8.14 - What is the minimum number of coins (same size) required on a plane, so that we need four colors to color the coins?

  To simplify, first ask kids to draw a pattern which requires 3 colors, even though no three coins touch each other. Ask them to identify the kind of constraints that are requiring more than 2 colors. Now combine different types of constraints.

• Ask kids to visualize simple operations  such as addition, subtraction, multiplication and division

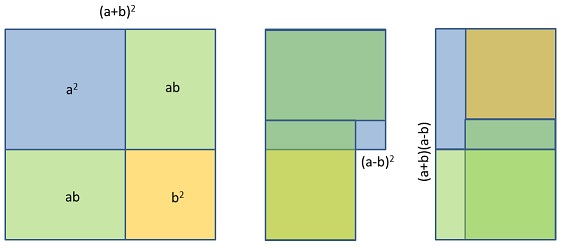
• Visualize (x-4)*(x+2)

  Compute 96*1002
• Visualize a^3 (cube of a) in 3D and 2D
• Ask kids to visualize (a+b)^3 (cube of a+b) - in 3D

  Can kids translate this visualization into 2D?

• 5 rational pirates find 100 coins. Seniority A to E. Senior pirate proposes, then everyone votes. If approved by majority or tie, it happens, else proposer is thrown and process restarts. All else equal, pirates like to throw. What is the best distribution for A to propose? 

  Answer: 98,0,1,0,1
• What if a tie doesnt work? 

  Answer: 97,0,1,0,2  or 97,0,1,2,0What if there are 6 pirates on these rules?Answer: 94,0,1,2,3,0 or 94,0,1,2,0,3

• 6 pirates, 1 coin, tie survives. What is Pirate 6's plan 

  Answer: Give to pirate 4; pirate 5 dies if he doesnt accept the plan!